Pulse Shape Download (Summary)

Selective Pulses

  • SURBOP90/SURBOP180: Selective Universal Rotation Pulses for Triple Resonance Experiments on 1.2 GHz Spectrometers

Conventional Broadband Pulses for Direct Applications

Broadband Pulses with Phase Slopes

  • SORDOR: Energy-Minimal Universal Rotations with Quadratic Phase Slope
  • RADFA: beta-Pulses with Variable Flip Angle and Linear Phase Slope for Ultimate Bandwidth
  • ICEBERG: Broadband Excitation with Linear Phase Slope for Pulse-Delay Applications

Systematic Studies of Pulse Shapes

Special Pulse Shapes

  • Pattern Pulses: Pulse Shapes with highly B0/B1 (Offset/RF-Amplitude) Dependent Profiles.

Historic Pulse Shapes

  • BEBOP: Initial broadband excitation pulses that served as role models for Optimal Control Theory in NMR spectroscopy and the development of the GRAPE algorithm

       

Details and Downloads

SURBOP90 and SURBOP180 (for Triple Resonance Experiments on 1.2 GHz Spectrometers)

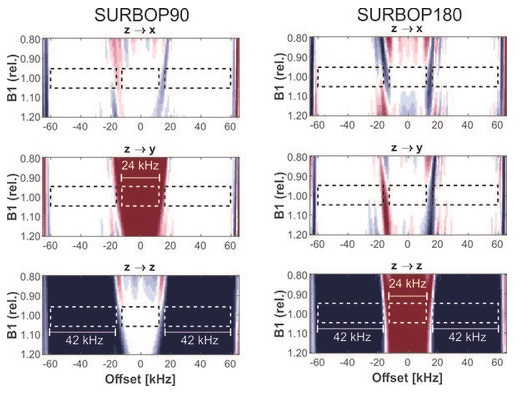Background: With the advancement of spectrometer field strengths, conventional triple resonance experiments need to cover larger and larger frequency bandwidths. With the latest spectrometer generation operating at 1.2 GHz 1H Larmor frequency, even selective pulses start to reach a limit: HNCACB and other protein triple resonance experiments require selective 90° and 180° pulses that cover the aliphatic carbon region, corresponding to approximately 24 kHz. Unfortunately, all commonly used selective pulse shapes cannot reach this bandwidth without violating the rf-amplitude specifications of available triple resonance probeheads.

Our recently optimized SURBOP90 and SURBOP180 pulses have a higher ratio of selective bandwidth to maximum rf-amplitude than standard pulses, enabling the implementation of critical triple resonance experiments on 1.2 GHz spectrometers. The pulses generally perform better than standard pulses, like e.g. Q3/Q5, and have been tested successfully in HNCACB-type experiments.

 

 

Downloads:

SURBOP90 (24 kHz BW, 15 kHz RF, +/-5% B1, 333 us)

SURBOP180 (24 kHz BW, 15 kHz RF, +/-5% B1, 333 us)

Hints/Instructions: The nominal rf-amplitude of 15000 Hz corresponds to a hard 90° pulse of duration tp=1/(15000 Hz * 4)=16.66us. Please calculate or calibrate the power level of a 16.66us hard pulse and use it to specify the corresponding power level of the shaped pulses (spwX or spdbX on Bruker spectrometers) with a pulse duration of 333us. 

Both pulses are saved in the old Bruker TopSpin pulse shape format. Please load them into the shape tool (stdisp) and save them for actual use. Experimental offset profiles of the pulses in JCAMP-DX format can be found here:

Offset profile of SURBOP90 

Offset profile of SURBOP180 

 

Example pulse shapes optimized using analytical exact gradients

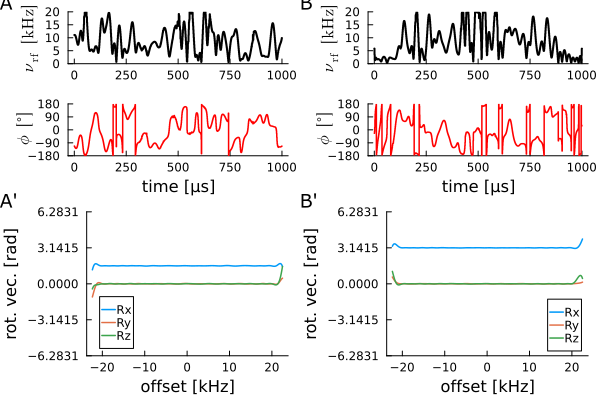Background:  exact analytical gradients for simple rotation matrices and quaternions have been introduced either with x,y / x,y,z / a,p / a,p,z / p controls (Cartesian and polar coordinates) as well as with holonomic pseudo controls based on hyperbolic tangent bounding (S. Slad and B. Luy, Ref. ). In the manuscript several pulse shapes have been optimized to analyze runtime and convergence properties of the analytical approach. Julia programs with analytical solutions can be found under Downloads/Others. Pulse shapes in .xyzt format (x-control, y-control, z-control, time) can be downloaded here:

15N_pulses_(6kHz_bandwidth) .zip

13C_pulses_(40kHz_bandwidth) .zip

19F_pulses_(120kHz_bandwidth) .zip

 

BURBOP-90 and BURBOP-180 for 19F Applications

 

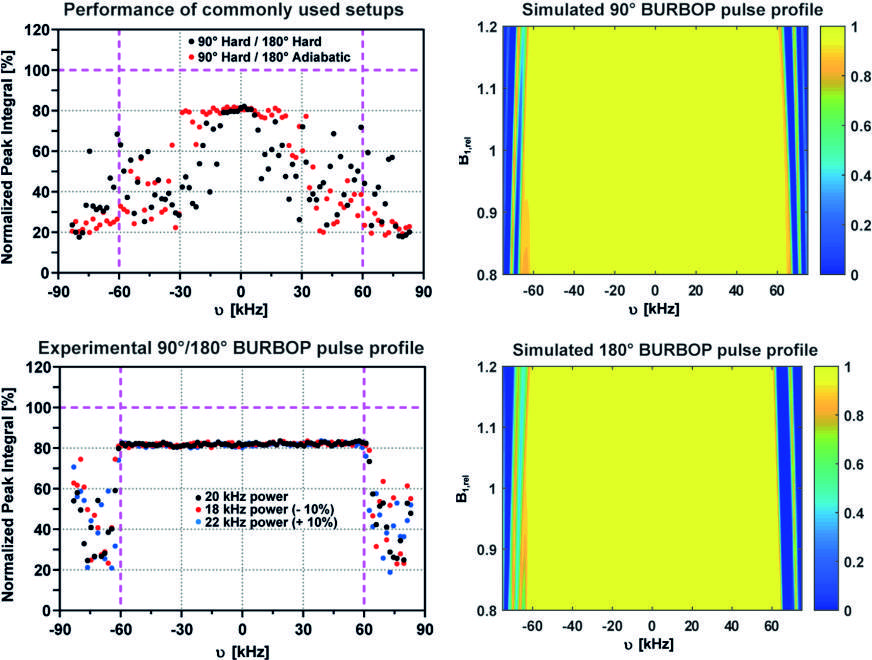Background: 19F applications, like 19F-based drug screening using CPMG-type experiments, require a very large chemical shift bandwidth to be covered (A. Lingel et al., Angew. Chem. Int. Ed. 59, 14809–14817 (2020), Ref. 207). An analysis shows that a bandwidth of approximately 200 ppm (-40 ppm to -240 ppm) is sufficient to cover the chemical diversity of most fluorine compounds. On a 600 MHz spectrometer this corresponds to ca. 113 kHz. We therefore designed robust high performance BURBOP-90° and BURBOP-180° pulses (so-called universal rotation 90° and 180° pulses) with a bandwidth of 120 kHz and an rf-amplitude of 20 kHz that is available on most modern 19F probeheads.

The performance of the pulse shapes is shown to the left in both experiment and theory. The experimental comparison with hard pulses or a combination of hard 90° and adiabatic refocusing on the left clearly shows the vastly improved performance of the BURBOP combination (the reduction of signal intensity to about 80% is due to relaxation in the 120ms CPMG test experiment). The yellow areas in pulse performance simulations, on the other hand, demonstrate the exceptional robustness against B1-field inhomogeneities of +/- 20%.

Downloads: Pulse shapes for Bruker spectrometers can be downloaded here:

F19-BURBOP-90(120kHz BW, 20kHz RF, +/-20% B1, 600us)

F19-BURBOP-180(120kHz BW, 20kHz RF, +/-20% B1, 1ms)

Hints/Instructions: The nominal rf-amplitude of 20000 Hz corresponds to a hard 90° pulse of duration tp=1/(20000 Hz * 4)=12.5us. Please calculate or calibrate the power level of a 12.5us hard pulse and use it to specify the corresponding power level of the shaped pulses (spwX or spdbX on Bruker spectrometers) with a pulse duration of 1ms. 

Just in case: If a given probehead does not allow a hard pulse of 12.5us, the F19-BURBOP pulses can still be applied with reduced rf-amplitude, but also reduced bandwidth. Assume a shortest possible hard pulse of 16us, i.e. 1.28*12.5us. The BURBOP-Pulses applied with this power level and a pulse duration of 1.28ms will then cover a bandwidth of ca. 94 kHz or 164 ppm on 19F on a 600 MHz spectrometer.

The pulse can also be applied instead with the 16us power level and slightly reduced performance with a pulse duration of 1.1ms. In this case, still a bandwidth of 120kHz/1.1=109kHz is achieved, sufficient for most applications, but with a smaller compensation against B1-inhomogeneity.

 

Best Broadband Pulses for 1H,13C Pulse Sequences: Taking 1JCH into Account

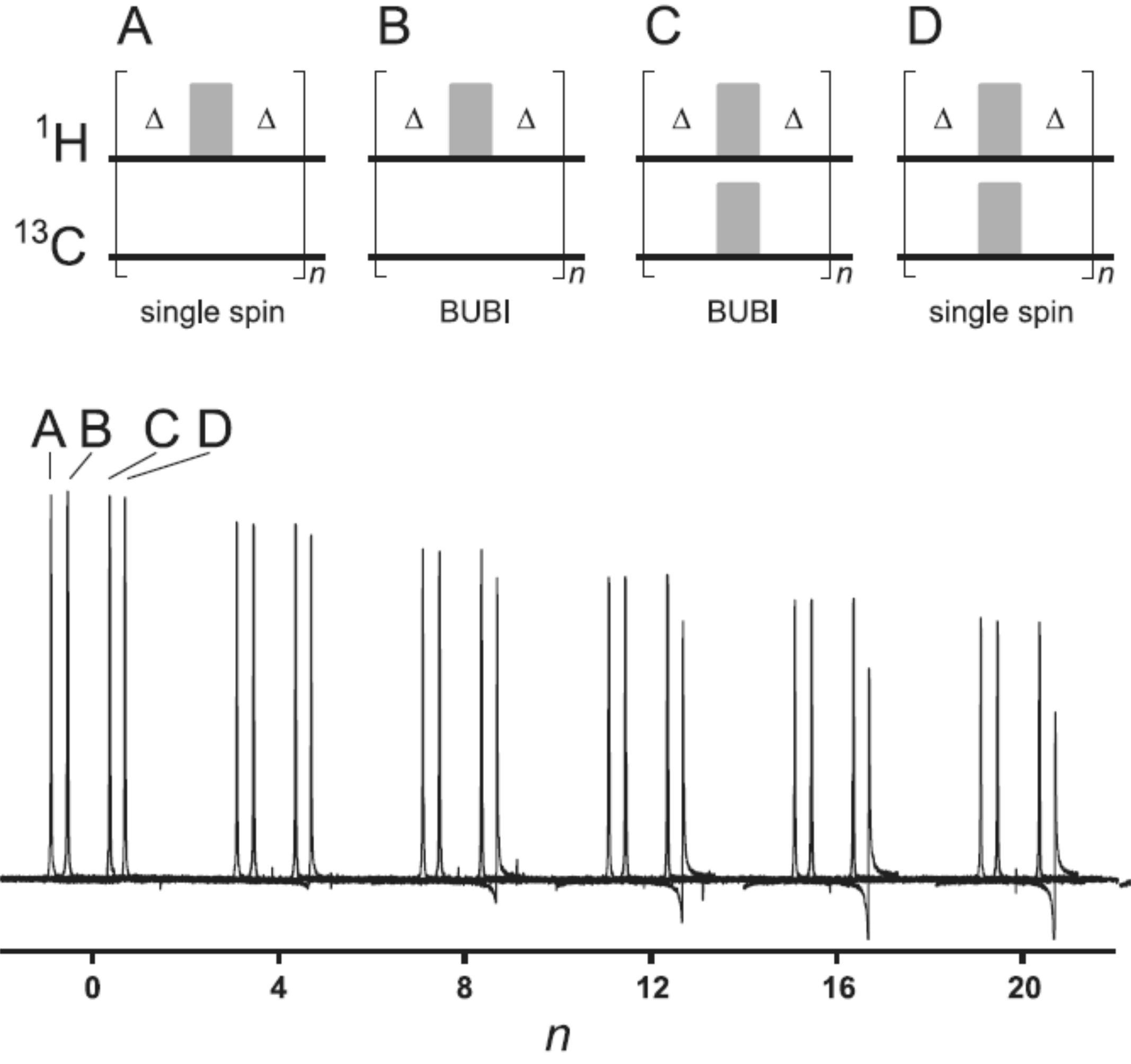Background: Broadband pulses are usually optimized considering a single spin 1/2, simply because optimizations for higher spin systems are very costly in terms of computing time. As long as a single pulse is applied at a certain time, heteronuclear coupling evolution follows the phase of the pulse and does not need to be considered. Homonuclear couplings, instead, are always present, but usually for protons can be neglected because pulse lengths are short compared to 1/JHH. However, W. Bermel was the first spectroscopist to report to us that BEBOP pulses do not perform as good as in theory in certain heteronuclear experiments. It took us a long time to figure out the reason for this. We did simulations and resulting quality factors for pulses changed only slightly when heteronuclear couplings on the order of 125Hz to 250 Hz were considered (the figure left shows a CPMG-type element with the slight drop in wanted magnetization when single spin-optimized pulses are compared with BUBI as described below). Still, experimentally drops in sensitivity of 10%, sometimes even up to 30% were observed, depending on the sequence used and couplings being present. Finally, we understood, that not the correctly transferred magnetization is the problem (which is essentially unchanged according to the quality factor), but the produced unwanted coherences, which eventually switch sign and lead to signal subtraction.

We therefore optimized two pulse sandwiches for the most frequently occurring simultaneously applied pulses in heteronuclear experiments: i) the application of a proton refocusing pulse and the corresponding application of a carbon inversion pulse, and ii) the simultaneous application of an excitation and a time-reversed excitation pulse on protons and carbons, respectively. As these pulses correspond to the application of a BURBOP(1H)/BIBOP(13C) and BEBOP(1H)/BEBOPtr(13C), we called the corresponding pulse sandwiches BUBI and BEBEtr. As corresponding pulse sandwiches required the optimization of all combinations of 1H and 13C offsets and B1-field ranges, as well as variations in the heteronuclear 1JCH couplings, optimizations on a 16-core Linux cluster took more than 90 days for each pulse sandwich. Nevertheless, resulting pulse shapes cover 10 kHz on protons and 37.5 kHz on carbons with an unprecedented robustness on both nuclei. We use the pulses with exceptional performance as pulse sandwiches, but also as individually applied pulse shapes on both 1H or 13C whenever applicable. 

Downloads: The two BUBI pulse shapes for Bruker spectrometers can be downloaded here:

F19-BURBOP-90(120kHz BW, 20kHz RF, +/-20% B1, 1ms)

F19-BURBOP-180(120kHz BW, 20kHz RF, +/-20% B1, 1ms)

Corresponding pulse shapes for BEBEtr can be found here:

 

J-Compensated Transfer Elements

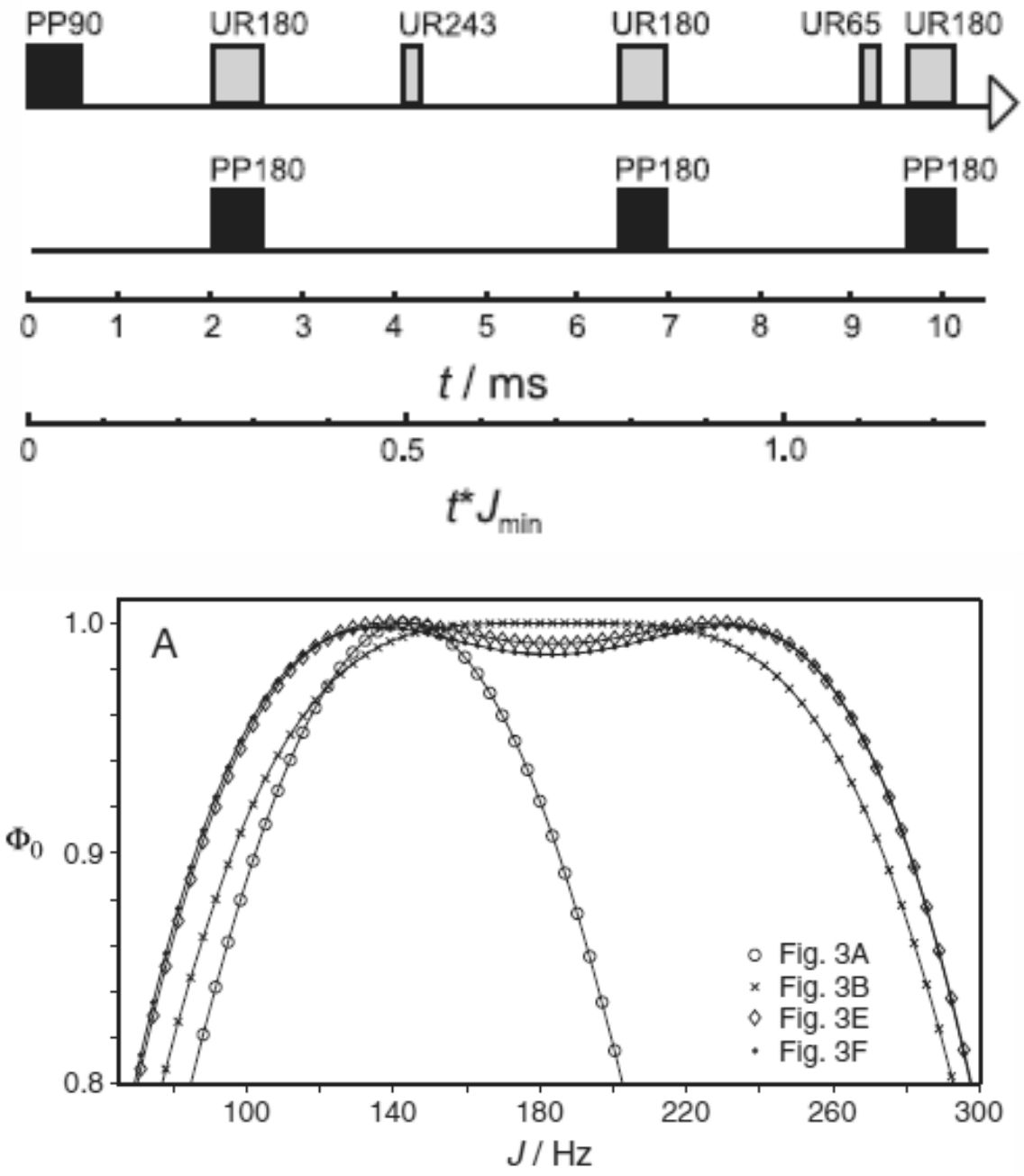Background for COB: It happens regularly that an organic chemists comes in our laboratory and says "I don't understand my NMR spectra". Usually, the chemist has some problem with data interpretation that can be solved with standard methods, but sometimes also peaks appear at positions, where there should be none, or resonances, for which cross peaks are expected, do not show up in corresponding spectra. This especially happens, when structures with triple bonds appear, for which 1JCH couplings are on the order of 250 Hz instead of 125-160 Hz they are usually expected. As a result, all heteronuclear transfer elements are misset by almost a factor 2, which causes the observed disappearance in HSQC/HMQC-type experiments and the occurrence of unexpected peaks in HMBC-type experiments. We therefore invested into a "failsafe" transfer element that would cover all commonly occuring variations in 1JCH couplings, 1H,13C-offsets, and B1-inhomogeneities (S. Ehni and B. Luy, Magn. Reson. Chem. 50, S63-S72 (2012), Ref. 100)The resulting pulse sequence and its theoretical performance is shown in the figure on the left hand side together.

Downloads COB: The 1H-part of the BEBEtr pulse sandwich is used for excitation (PP90, see above) and BUBI pulse sandwiches are used in all delays for refocusing/inversion (UR180 and PP180, see above) and additional 1H pulse shapes can be found here:

A systematic approach for optimizing the robustness of pulse sequence elements with respect to couplings, offsets, and B1-field inhomogeneities (99)

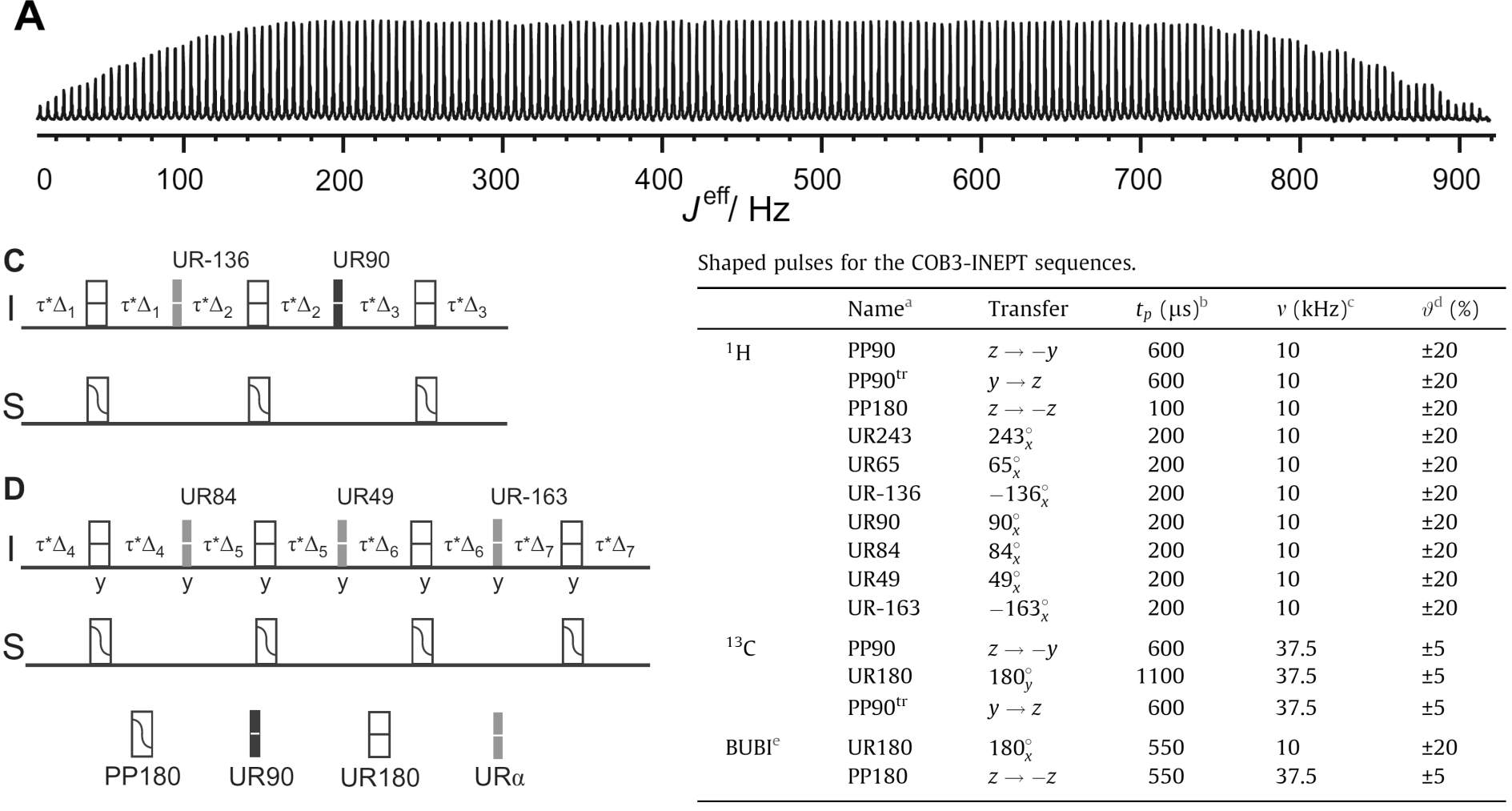Background for COB3: Following the successfull development of the COB sequence, we found that J-compensated transfer would be of even stronger interest for partially aligned samples with residual dipolar couplings on the order of several hundred Hz or for the back-transfer starting from 13C inphase magnetization for CH, CH2, and CH3 groups. We therefore did the same optimization procedure as for the COB experiment, but for the much wider coupling range of 120-750 Hz (S. Ehni and B. Luy, J. Magn. Reson. 247, 111-117 (2014), Ref. 125).

Downloads COB3: The 1H-part of the BEBEtr pulse sandwich is used for excitation (PP90, see above) and BUBI pulse sandwiches are used in all delays for refocusing/inversion (UR180 and PP180, see above) and additional 1H pulse shapes can be found here:

 

Highly Optimized Broadband Excitation and Refocusing Pulses

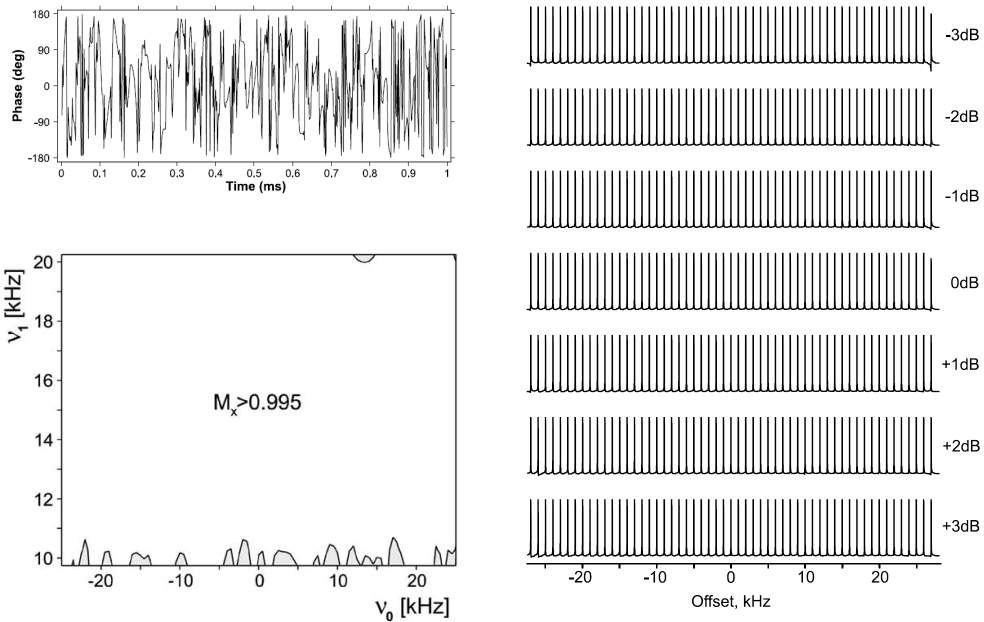Background and Downloads: Here, a collection of very good performing broadband pulses is given. The first pulse, also termed "miracle pulse" (see pulse phase, theoretical and experimental performance to the left), provides excellent excitation over a bandwidth of 50 kHz and an extraordinary B1-range of 10-20kHz, resembling almost calibration-free excitation (T.E. Skinner et al., J. Magn. Reson. 179, 241-249 (2006), Ref. 51). It is also a constant-amplitude pulse, which is especially interesting if no linearized amplifiers are available. As with all excitation pulses, this is a point-to-point pulse optimized for the transfer z to x only. The time-reversed (tr) pulse accordingly achieves x to z transfer.

BEBOP(50kHz BW, 10kHz-20kHz RF, 1ms, Bruker format, transforms Iz to Ix).
BEBOPtr(50kHz BW, 10kHz-20kHz RF, 1ms, Bruker format, transforms Ix to Iz).

The corresponding refocusing pulse, also more systematically called a universal rotation 180° pulse, is given by the following constant amplitude BURBOP-180° pulse. Again, a bandwidth of 50 kHz is combined with an extreme B1-range of 10-20 kHz rf-amplitude with a quite short duration of 2 ms.
BURBOP-180o(50kHz BW, 10kHz-20kHz RF, 2ms, Bruker format).

A different version of a refocusing pulse with utmost performance and maximum rf-amplitude of 10-20 kHz (nominal 15 kHz) has been developed (T.E. Skinner et al., J. Magn. Reson. 216, 78-87 (2012), Ref. 92), for which a peak amplitude is allowed at the pulse center, corresponding to the physical needs of such pulses (B. Luy et al., J. Magn. Reson. 176, 179-186 (2005), Ref. 48). The overall rf-power/rf-energy of the pulse is as such significantly lower than the corresponding constant amplitude pulse. As "Burbop-180.1" it is now part of the Bruker standard pulse shape library where it outperforms the previously used composite CHIRP pulses.

BURBOP-180o(50kHz BW, 10kHz-20kHz RF, 2ms, Bruker format).

 

Broadband RADFA Pulses with Scalable Flip Angle beta

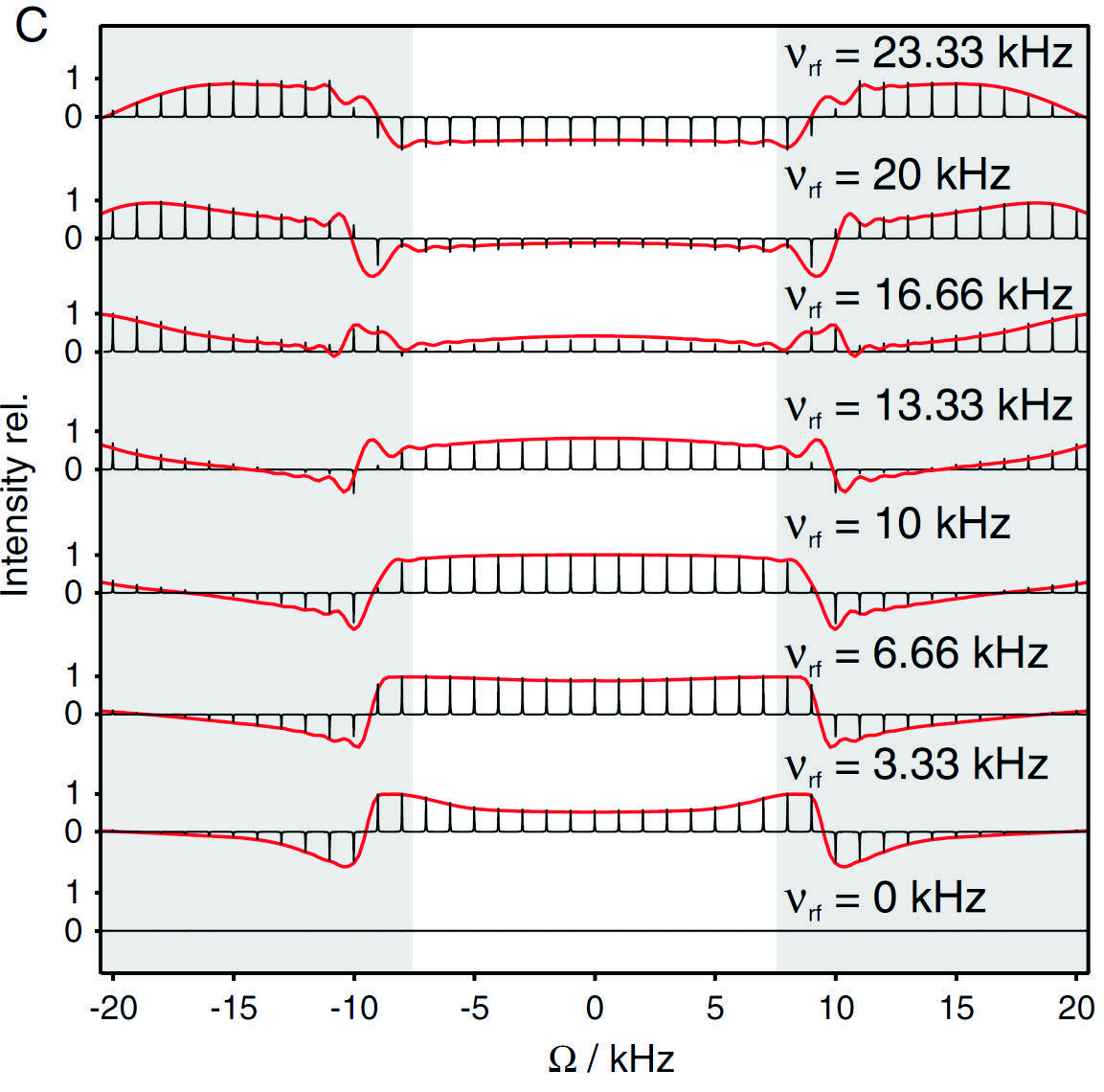Background: Conventional broadband excitation pulses are specified for an effective flip angle of 90°. However, pulse sequences with Ernst-angle excitation require variable effective flip angles, depending on the average relaxation properties of a specific sample. We therefore optimized pulse shapes that cover  a certain bandwidth with rf-amplitude dependent effective flip angle, just like conventional hard pulses. Pulses were designed for an effective rf-amplitude of 10000 Hz for a 90° excitation and 20000 Hz for corresponding 180° inversion.(M.R.M. Koos et al., Magn Reson Chem. 53, 886-893 (2015), Ref. 138) Every effective flip angle in between can be achieved by adjusting the rf-amplitude accordingly (see experimental (black) and theoretical (red) performance for an example pulse with 15 kHz bandwidth in the figure to the left).

Downloads RADFA: Selected RADFA pulses for broadband excitation with an effective flip angle b in the range of 0-180° can be found here:

 

SORDOR 90°/180° Universal Rotation Pulses with Quadratic Phase Slope

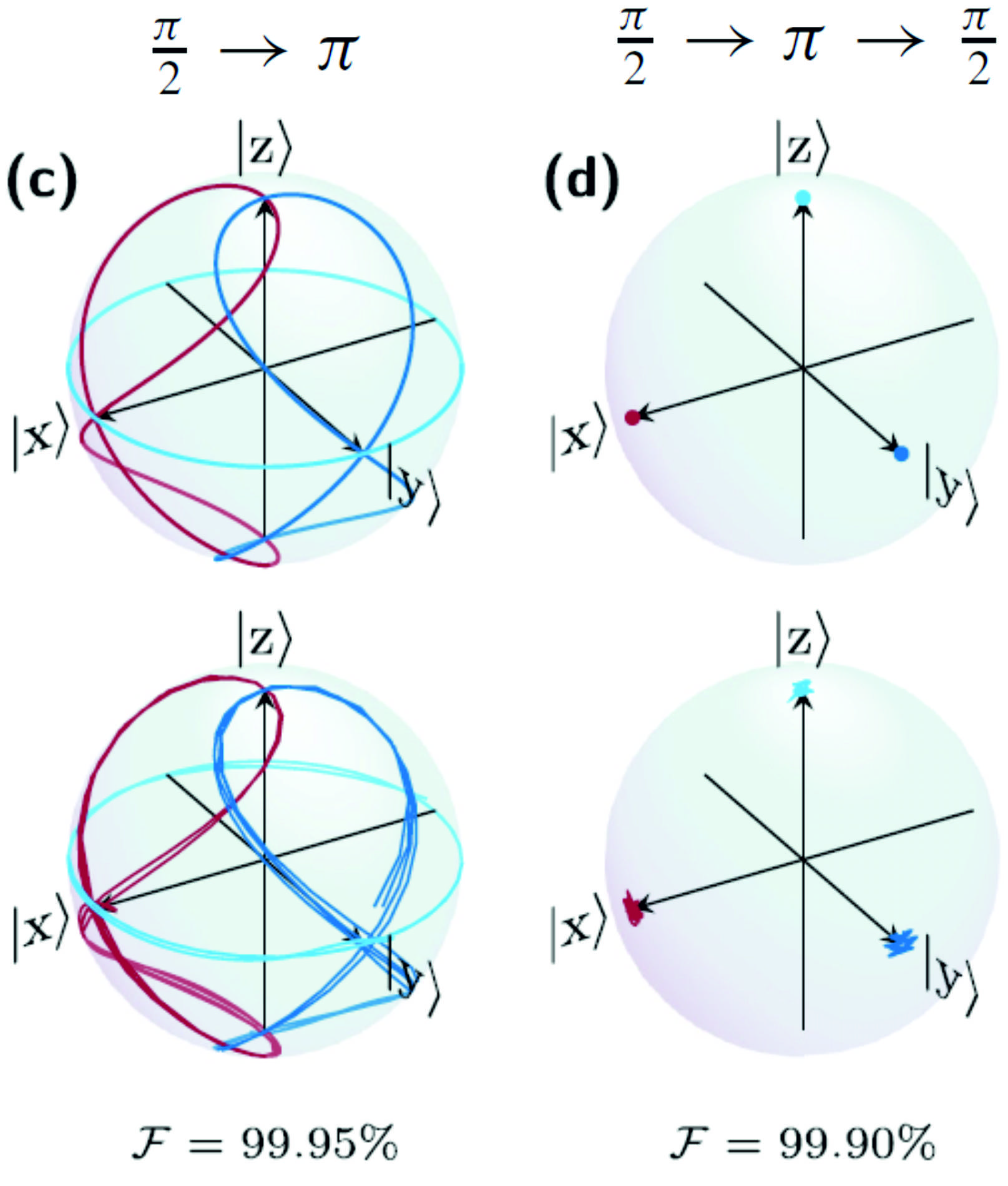Background: SORDOR pulses are a novel type of broadband universal rotation pulses that can be used in a cooperative fashion (D.L. Goodwin et al., Phys. Rev. Research 2, 033157 (2020), Ref. 204, J. D. Haller et al., Magn. Reson.  (2022), Ref. 219). Using the classical classification scheme by Malcolm Levitt, SORDOR pulses do not fulfill the requirements of B3 pulses with constant rotation axis and rotation angle, but fulfill higher requirements than B1 pulse class, i.e. pulses with a constant rotation angle but no defined rotation axis. Instead, SORDOR pulses have a constant rotation angle and well-defined, offset-dependent rotation axes in the x,y plane. With a typically quadratic phase, broadband refocusing pulses can be optimized with rf-energy requirements of an inversion pulse, i.e. only about 50% of the pulse length. The pulses are best used in a cooperative way with SORDOR-90 and SORDOR-180 pulses with identical offset dependencies of effective rotation axes. The effective rotation axes for the uncompensated SORDOR-90/SORDOR-180 and the compensated SORDOR-90/SORDOR-180/SORDOR-90 application are shown in the figure to the left.

Downloads: Example SORDOR pulse shapes can be downloaded here:

SORDOR-90(50kHz BW, 10kHz RF, 720us, pm 5% B1, Bruker format).

SORDOR-180(50kHz BW, 10kHz RF, 720us, pm 5% B1, Bruker format).

SORDOR-90(50kHz BW, 10kHz RF, 720us, pm 10% B1, Bruker format).

SORDOR-180(50kHz BW, 10kHz RF, 720us, pm 10% B1, Bruker format).

See also the systematic pulse shape studies section for a wide range of optimized SORDOR pulse shapes.

 

RADFA Pulses with Linear Phase Slope

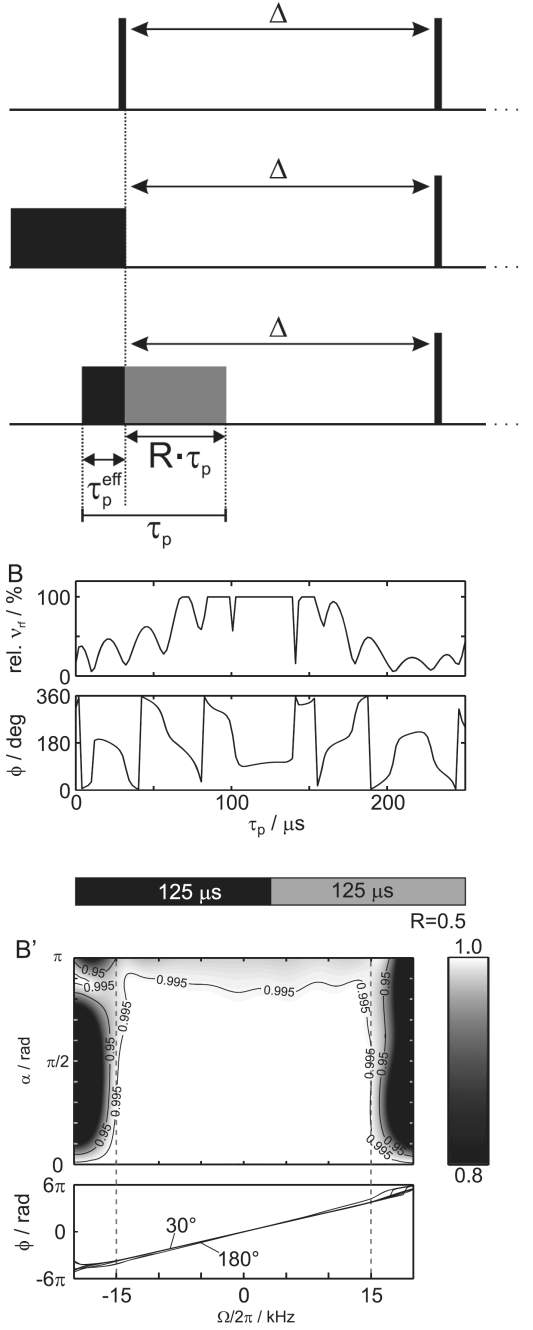Background: Constant phase RADFA pulses (see above) allow broadband excitation with a β-flip angle (0°-180°) depending on the applied rf-amplitude. However, pulse performance is limited especially for larger bandwidths. RADFA pulses allowing a linear phase slope can reach much higher bandwidths (M.R.M. Koos et al., Magn. Reson. Chem. 55 (9), 797-803 (2017), Ref. 164). With the R-factor the fraction of the pulse is defined that corresponds to the effective delay within the pulse that has to be used to adjust a delay Δ in a pulse-delay sequence (see figure to the left). Corresponding pulses allow very wide excitation bandwidths of up to 50 kHz, unreachable by corresponding constant phase RADFA pulses.

Downloads RADFA II: A selection of linear phase slope RADFA pulses can be found here:

 

 

Hints/Instructions: All RADFA pulses are optimized for a nominal rf-amplitude of 10000 Hz for an effective β=90° flip angle. A corresponding 45° excitation would be achieved with an rf-amplitude of 5000 Hz, a 180° inversion by an rf-amplitude of 20000 Hz, etc. . 

Bandwidth scaling can be achieved by changing pulse lengths and rf-amplitudes correspondingly. Twice the bandwidth, e.g., can be achieved with half the pulse length, but twice the rf-amplitude. The phase slope is then the same, but over the doubled bandwidth, as if also the effective delay is half. This is a result of the fact that the effective delay is always R*tP. 

 

ICEBERG Pulses with Linear Phase Slope

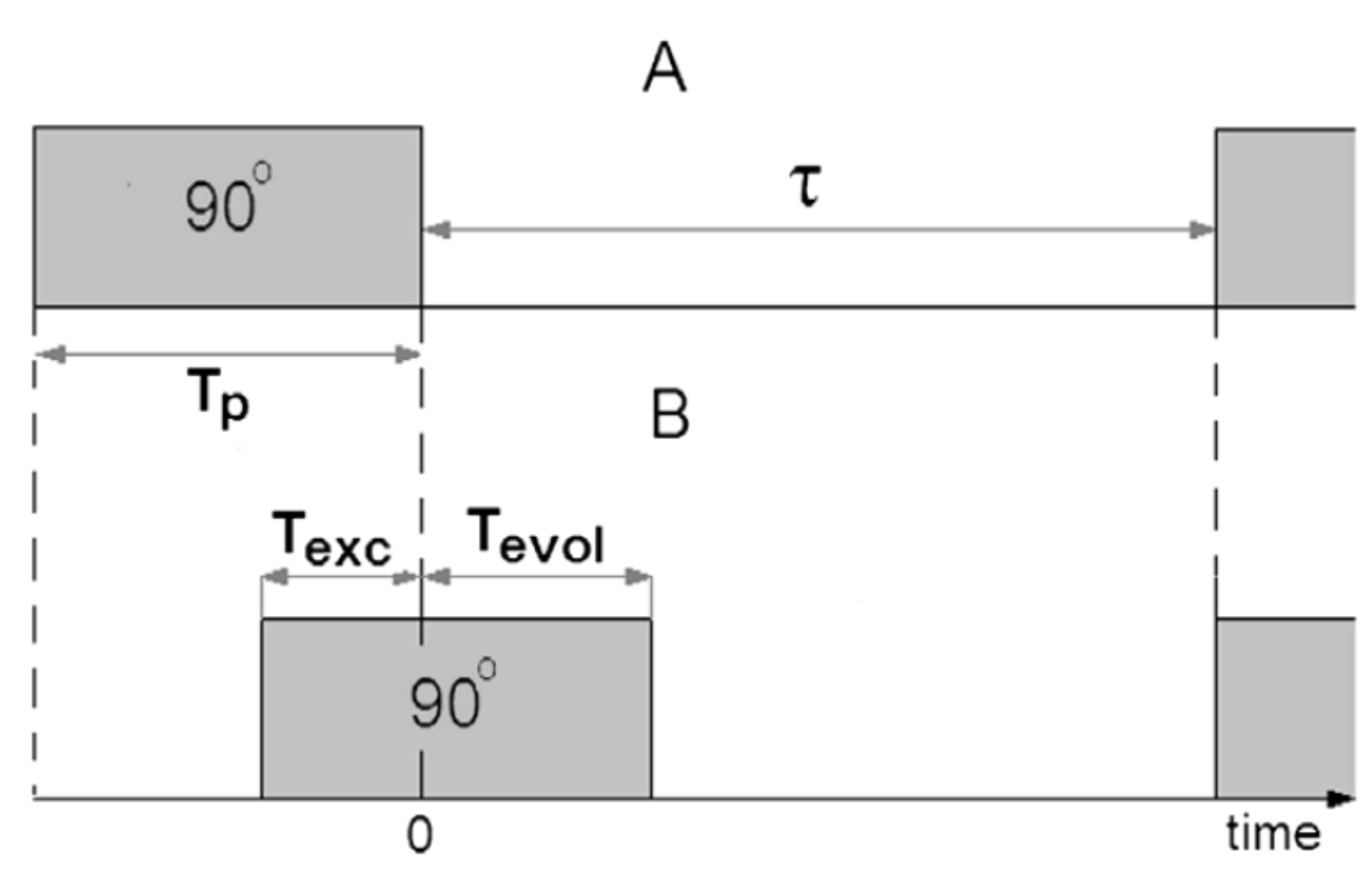Background: Conventional excitation pulses are applied in position of a 90° hard pulse. The pulse length usually is significantly longer than a corresponding hard pulse. In most situations this can be tolerated, but whenever fast relaxation takes place, the pulse length of the overall sequence must be strictly kept to the abolute minimum. Therefore ICEBERG excitation pulses have been developed for pulse-delay sequences, where the pulse itself is already part of the delay τ that follows the excitation (see figure to the left). The overall pulse sequence duration can thereby be reduced by the effective timespan τevol. This can be achieved by taking a linear phase slope into account during pulse optimization (N.I. Gershenzon et al., J. Magn. Reson. 192, 235-243 (2008), Ref. 64). If the delay τ is adjusted correspondingly, the ICEBERG pulse can be applied the same way as conventional excitation pulses.

Downloads: A selection of ICEBERG pulses can be found here:

 

Exploring the Limits of Broadband 90°/180° Universal Rotation Pulses

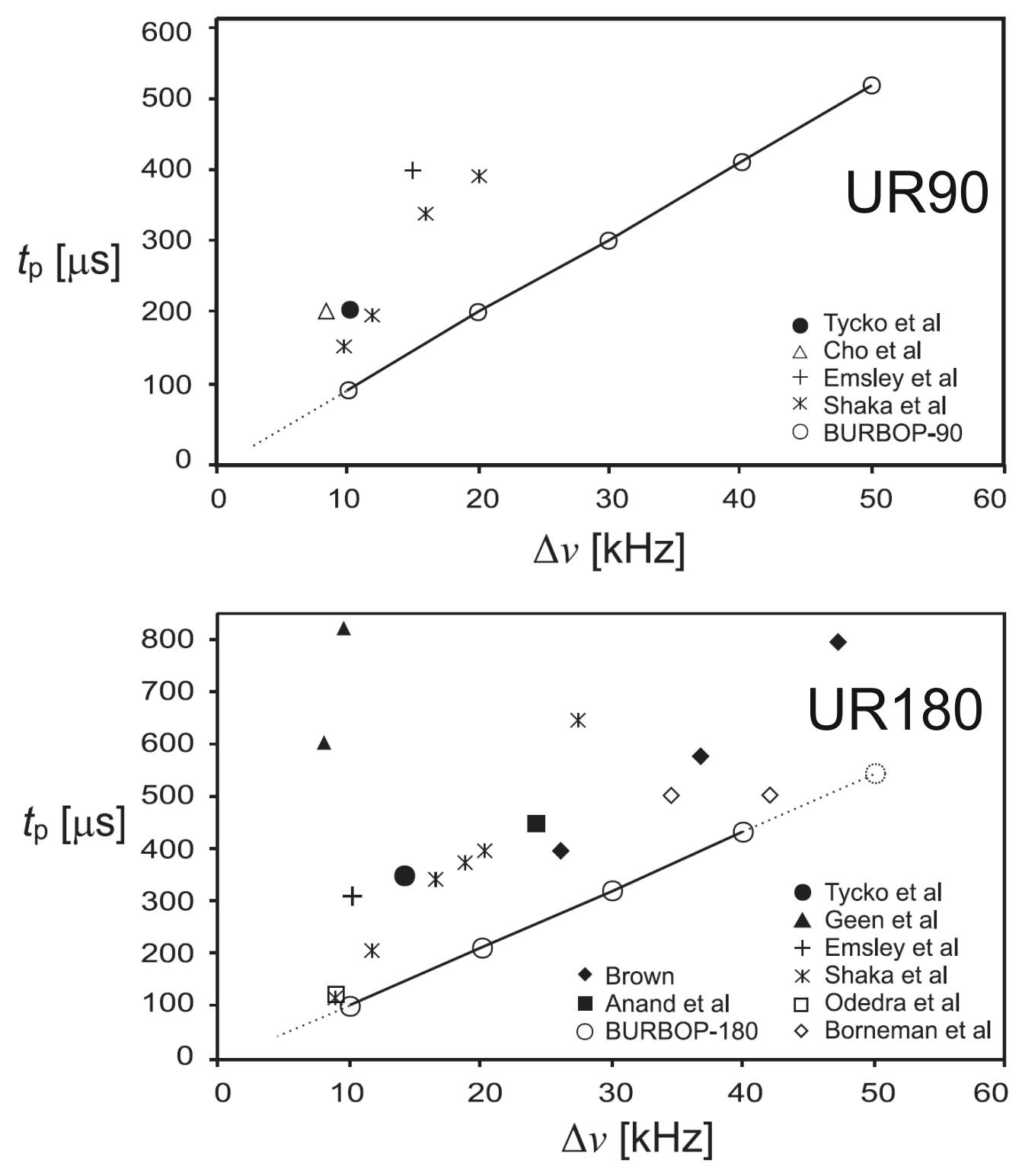Background: Next to point-to-point pulses like excitation (z -> x) and inversion (z-> -z) pulses, also universal rotation pulses are of highest interest in modern NMR spectroscopy, as they can be used directly as a replacement for hard pulses without knowledge of actual spin density operators being active. Universal rotation 180° pulses (UR180) are classically called refocusing pulses, while universal rotation 90° pulses (UR90) do not have any trivial name. Time to look into the physical limits of broadband UR90 (BURBOP-90) and UR180 pulses (BURBOP-180). It turns out that better performing pulses than existing pulse shapes are easily optimized (see figure to the left with open circles and solid lines indicating newly optimized BURBOP pulses). In addition, symmetry principles (B. Luy et al., J. Magn. Reson. 176, 179-186 (2005), Ref. 48) for the obtained pulses are being determined and demonstrated that a single UR180 usually shows equal or better performance than a pair of inversion pulses (K. Kobzar et al., J. Magn. Reson. 225, 142-160 (2012), Ref. 97).

Downloads: The collection of all best pulses for a given combination of bandwidth, rf-inhomogeneity, and pulse length, standardized to a maximum rf-amplitude of 10000 Hz,  can be downloaded here:

Exploring the Limits of Broadband 90° and 180° Universal Rotation Pulses (97)

 

Exploring the Limits of RF-Power-Limited Excitation and Inversion Pulses

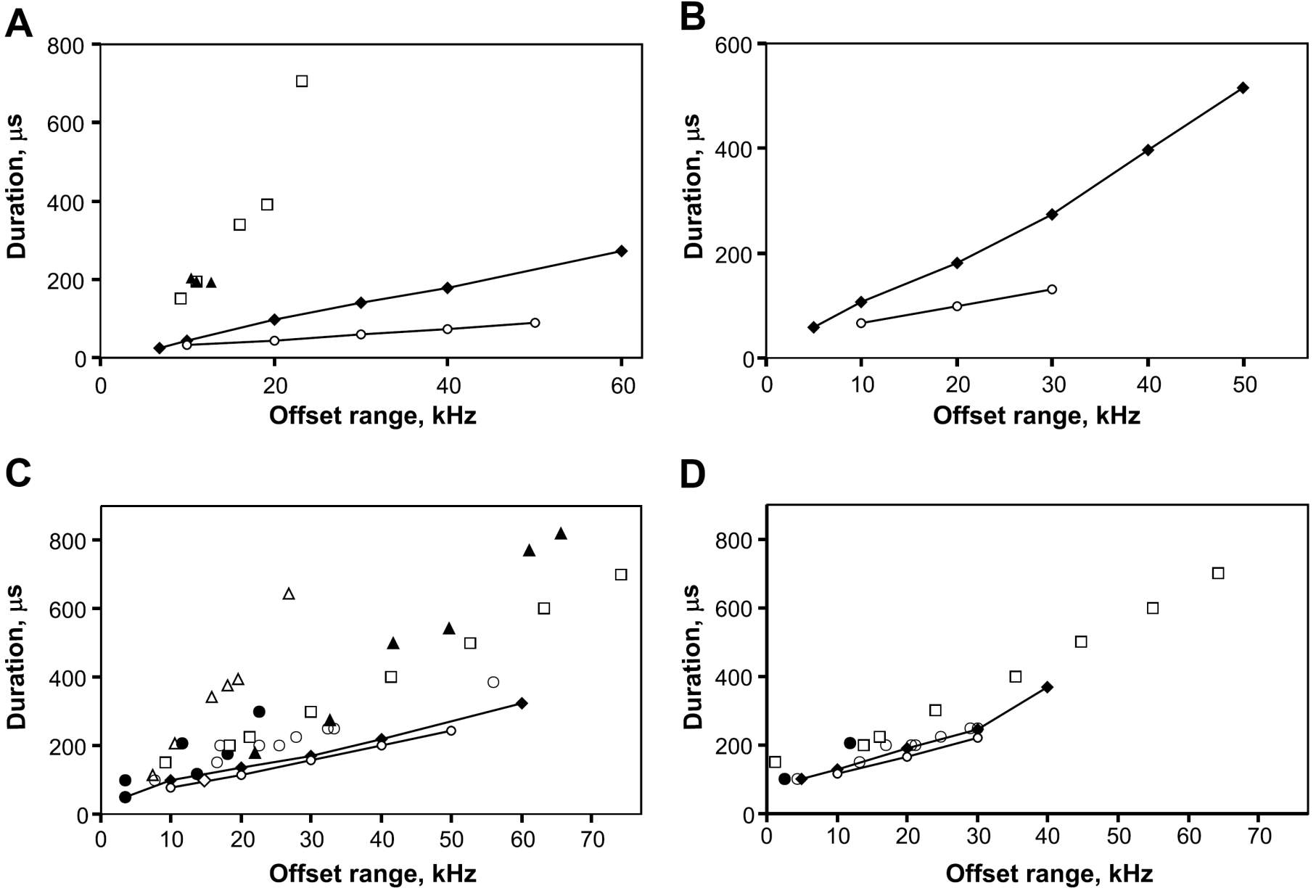Background: Broadband excitation and inversion pulses are widely used in modern NMR spectroscopy. Usually, rf-amplitude limited pulse shapes are optimized and used in applications. However, applications in imaging, but also within pulse trains like CPMG or decoupling sequences in spectroscopic applications make it necessary to apply pulses with minimal rf-power. We therefore repeated the exploration of physical limits of broadband excitaton and inversion pulses, this time with rf-power-limited pulse optimizations. The resulting power-BEBOP (excitation, empty diamonds and solid lines on the left, A and B) and power-BIBOP pulses (inversion, empty diamonds and solid lines on the left, C and D) compared to rf-amplitude-limited BEBOP and BIBOP pulses with identical rf-power (both with filled diamonds and solit lines on the left) reach equal performance with shorter pulse lengths and are highly interesting alternatives. Pulse shapes are compared to previously published excitation and inversion pulses without (A,C) and with +/-20% (B,D) B1-inhomogeneity (K. Kobzar et al., J. Magn. Reson. 194, 58-66 (2008), Ref. 66).

Downloads: The collection of all best pulses for a given combination of bandwidth, rf-inhomogeneity, and pulse length with the rf-power standardized to a 10000 Hz constant amplitude pulse can be downloaded here:

Power-BEBOP / Power-BIBOP rf-power limited excitation and inversion pulses from "Exploring the limits..." (66)

 

Exploring the Limits of RF-Amplitude Limited Excitation and Inversion Pulses

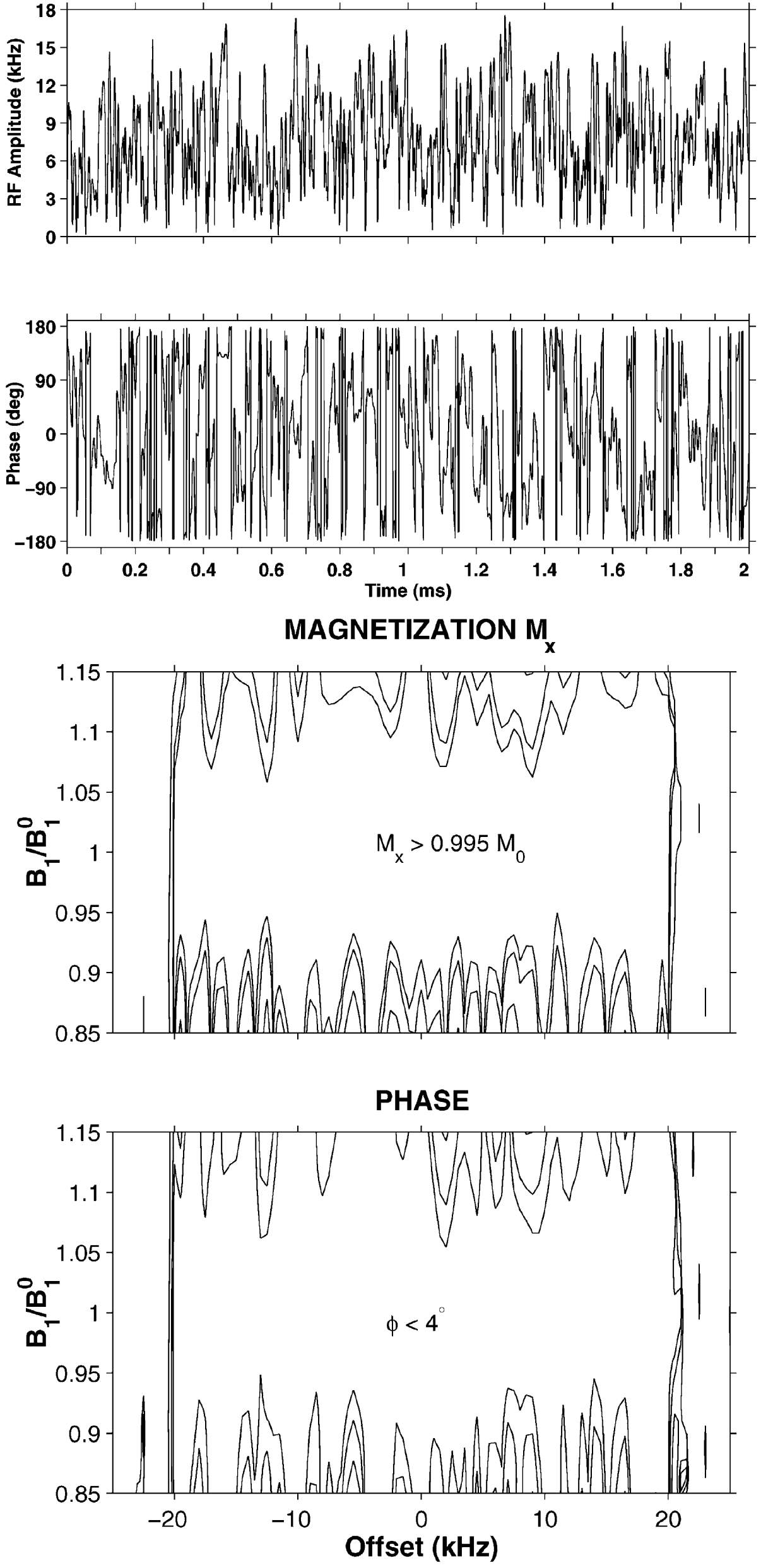
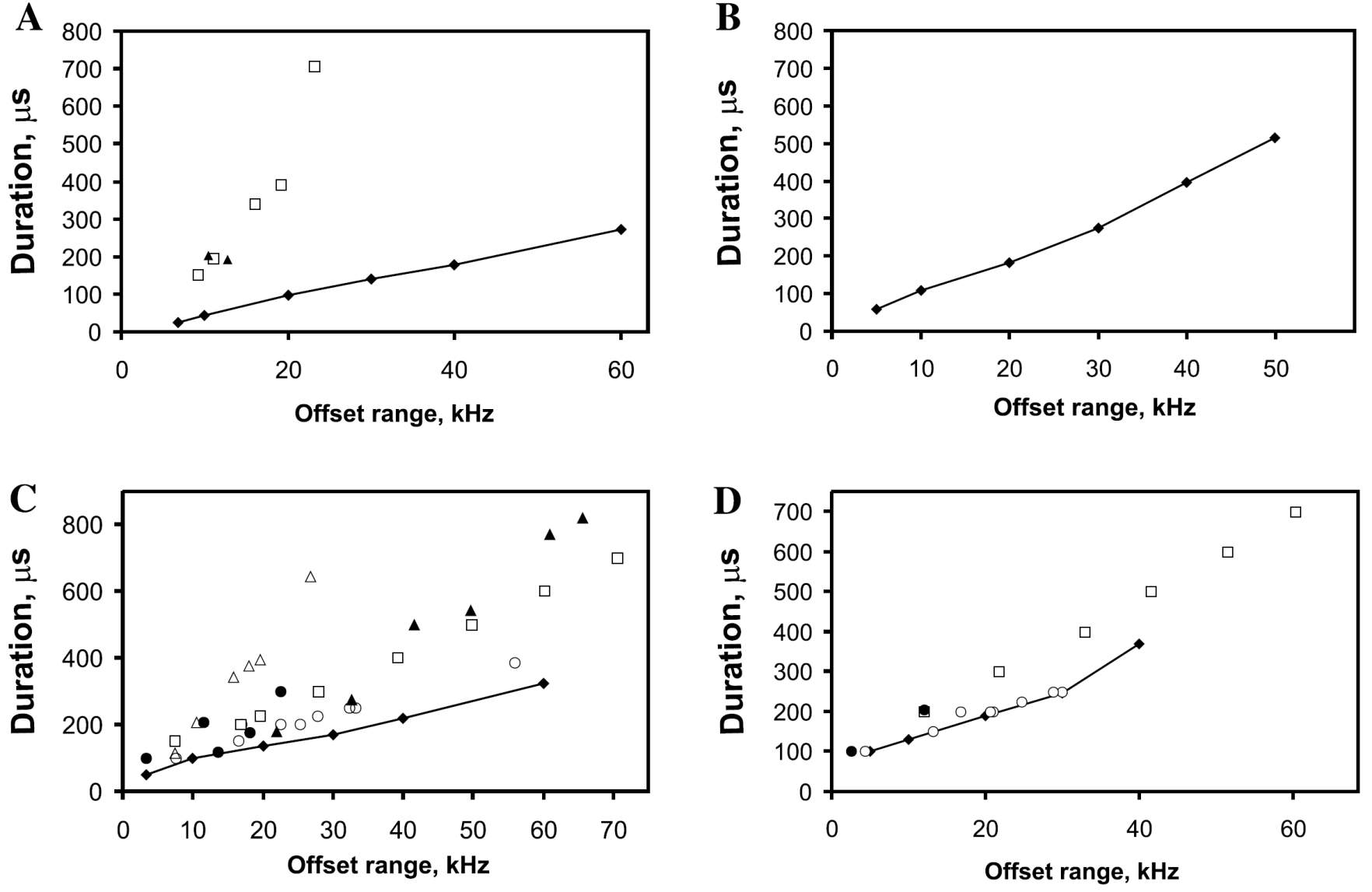Background: Many excitation and inversion pulses have been developed over decades with very different performances. It has been completely unclear in how far a pulse shows a very good or only a modest performance. With the advent of optimal control, it has been possible for the first time to do an overall screening of pulse performances, as the fast and well-converging algorithms allow optimizations within few hours. As the very initial paper of many "Exploring the Limits ..." publications, more than 100000 individual optimizations were carried out to get an estimate of the physical limits of broadband excitation and inversion (K.Kobzar et al., J. Magn. Reson. 170, 236-243 (2004), Ref. 37). The comparison of pulse performance of obtained BEBOP and BIBOP pulses with that of previously published excitation and inversion pulses is shown to the left (filled diamonds connected with solid lines: obtained BEBOP excitation (A,B) and BIBOP inversion pulses (C,D); without (A,C) and with +/-20% B1-inhomogeneity (B,D); previously published pulse shapes are indicated with other symbols, taken from Ref. 37).

Downloads: The collection of all best pulses for a given combination of bandwidth, rf-inhomogeneity, and pulse length with the standardized maximum rf-amplitude of 10000 Hz can be downloaded here:

BEBOP / BIBOP amplitude-limited excitation and inversion pulses from "Exploring the limits..." (37)

 

Pattern Pulses

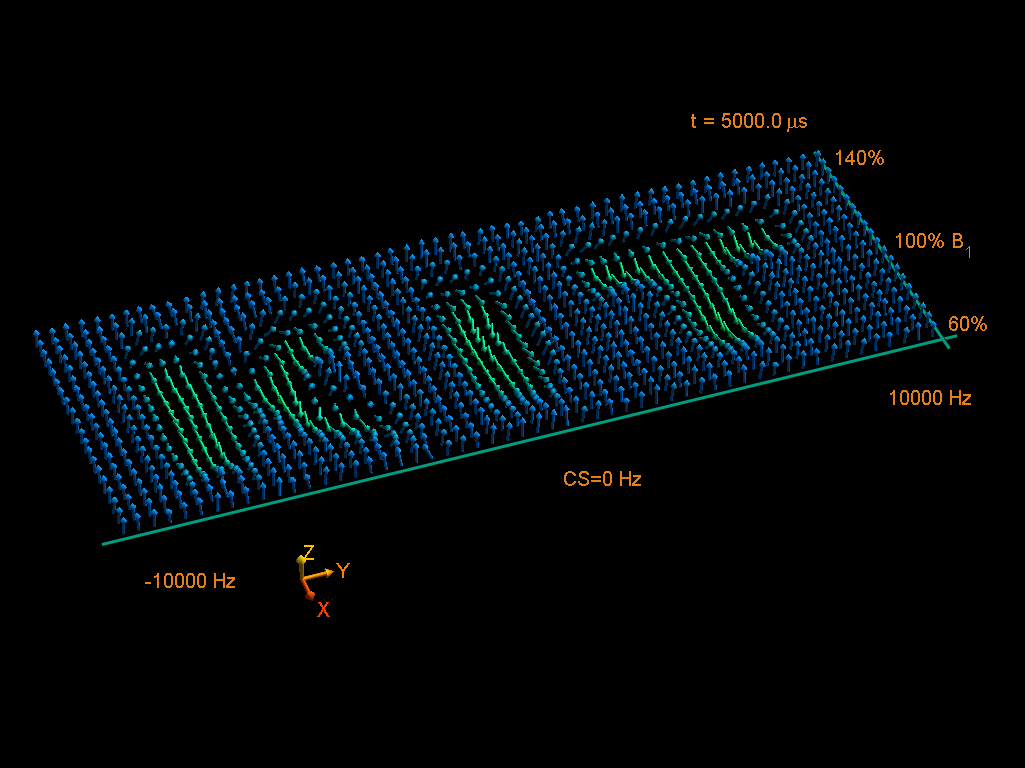Background: Pulse shapes are usually optimized for a certain bandwidth (B0-field) and a range of field inhomogeneities (B1-field). Band-selective or B1-selective pulse shapes are known, but also pulses with correlated B0/B1-selectivity are possible and introduced by the name Pattern Pulses. A very nice example is the KIT pulse to the left: (B0/B1)-specific green arrows indicate excitation and blue arrows no excitation and together they form the KIT pattern. By now quite a large number of corresponding Pattern Pulses have been optimized, mostly for demonstration purposes.

Downloads: The collection of different Patterns with corresponding Pattern Pulses can be found on this website:

Pattern pulses

 

Historic BEBOP Pulses: Role Model for Optimal Control in NMR

Background: BEBOP broadband excitation pulses were the initial optimization targets on which the predecessor algorithms of the important GRAPE algorithm were developed. The very first BEBOP pulses were optimized without any constraints on rf-amplitudes and led to 2 ms long pulses with a maximum rf-amplitude of 17.5 kHz, covering a bandwidth of 40 kHz. This was a milestone in pulse development as the best known pulses back then, the ABSTRUSE pulses, were pretty new and needed 6 ms and slightly larger rf-amplitudes to achieve the same goal. It was also one of the first pulses with a "noise-like" shape, but highly defined performance. Apparently, this type of pulses is best for the target and would never be obtained with classical optimization procedures with limited independent variables. Corresponding pulse shapes can be found here:

Broadband excitation pulses (Ref. 26)

BEBOP(40kHz BW, 17.5kHzRF, 2ms, Bruker format).
BEBOP(40kHz BW, 17.5kHzRF, 2ms, Varian format).

The first pulses with boundary conditions, i.e. rf-amplitude restricted pulse shapes, made it then possible to further reduce pulse durations by another factor 4, resulting into first highly applicable broadband excitation pulses:

Broadband excitation pulses (Ref. 33)

BEBOP(40kHz BW, 17.5kHzRF, 400us, 0.5us digitization, Bruker format).
BEBOP(40kHz BW, 17.5kHzRF, 400us, 0.5us digitization, Varian format).
BEBOP(40kHz BW, 17.5kHzRF, 500us, 0.5us digitization, Bruker format).
BEBOP(40kHz BW, 17.5kHzRF, 500us, 0.5us digitization, Varian format).
BEBOP(40kHz BW, 17.5kHzRF, 500us, 5us digitization, Bruker format).
BEBOP(40kHz BW, 17.5kHzRF, 500us, 5us digitization, Varian format).

But also this was just a start. BEBOP pulses further served as a starting point to look for component-selective optimization (T.E. Skinner et al., J. Magn. Reson. 172, 17-23 (2005), Ref. 40), a symmetry-based construction principle (B. Luy et al., J. Magn. Reson. 176, 179-186 (2005), Ref. 48), constant amplitude restraints (T.E. Skinner et al., J. Magn. Reson. 179, 241-249 (2006), Ref. 51), relaxation-optimized pulses (N.I. Gershenzon et al., J. Magn. Reson. 188, 330-336 (2007), Ref. 60), rf-power-optimizations (K. Kobzar et al., Ref. 66), pulses with a linear slope (N.I. Gershenzon et al., J. Magn. Reson. 192, 235-243 (2008), Ref. 64), and were the role-model for more recent quadratic phase slope SORDOR pulses (D.L. Goodwin et al., Phys. Rev. Research 2, 033157 (2020), Ref. 204).