Optimal Control Theory
The resonance frequencies of nuclei depend on their environment, which is different for each molecule and influenced by interactions with other nuclei and external fields. On the one hand this allows us to extract information about interactions; on the other hand uniform manipulation of all the spins becomes more difficult due to the resulting large frequency range. We aim to develop methods that enable such manipulations in order to design more efficient experiments.
Experiments in question utilise a multitude of different precise sequential spin manipulations. Depending on the experiment, different transfer steps have to be taken into account. Furthermore, spectrometer hardware itself has imperfections. The most severe ones are spatial inhomogeneities in the static magnetic field (B0) and the dynamic radio frequency field (B1). In many cases optimizations can include these deviations and yield robust pulses to prevent signal loss, artefacts and increase quality of the resulting spectra.
Optimal Control Theory and the GRAPE algorithm derived from it is an efficient method to optimize pulse sequences consisting of hundreds or thousands of parameters. This allows implementing all kinds of spin manipulations, provided they are physically possible. Optimal Control Theory has allowed us to develop pulses that achieve e.g. uniform excitation or inversion over large chemical shift bandwidth or pulses with compensation of B1 inhomogeneity, but also band-selective pulses, pulses depending on local B1 strength, pulses leaving magnetization in defined quantum states and optimized transfer elements.
Optimal control theory is a mathematical field that is concerned with control policies that can be deduced using optimization algorithms. This formalism is applicable in various different fields, from economics to space flghts. So, it is applied to find the optimal and least fuel-consuming trajectory for a rocket e.g. from Earth to the Moon. It also can be applied in NMR to optimize standard building blocks, accomodating and compensating different sources of signal losses, thus improving the sensitivity, as well as for designing completely new ones.
Read more about it also in wikipedia.
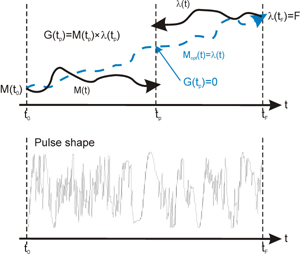
To find an extremum of a function of many variables, which is not defined analitically, one should be able to calculate gradients of this function with respect to all variables in every point of the multidimensional variable space. Optimal control theory provides an easy and fast method for that. In the easiest case of optimizing NMR RF-pulse one lets the magnetization evolve through the shape: from initial state to the end, and from the target state to the beginning of the shape. The cross-product of corresponding magnetization vectors is a gradient, wich one can use in a standard minimization algorithms, like e.g. steepest-descent.
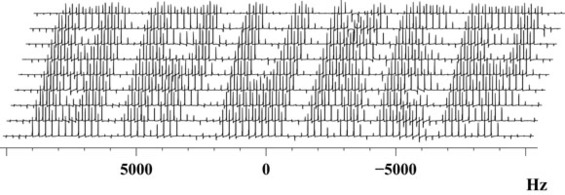
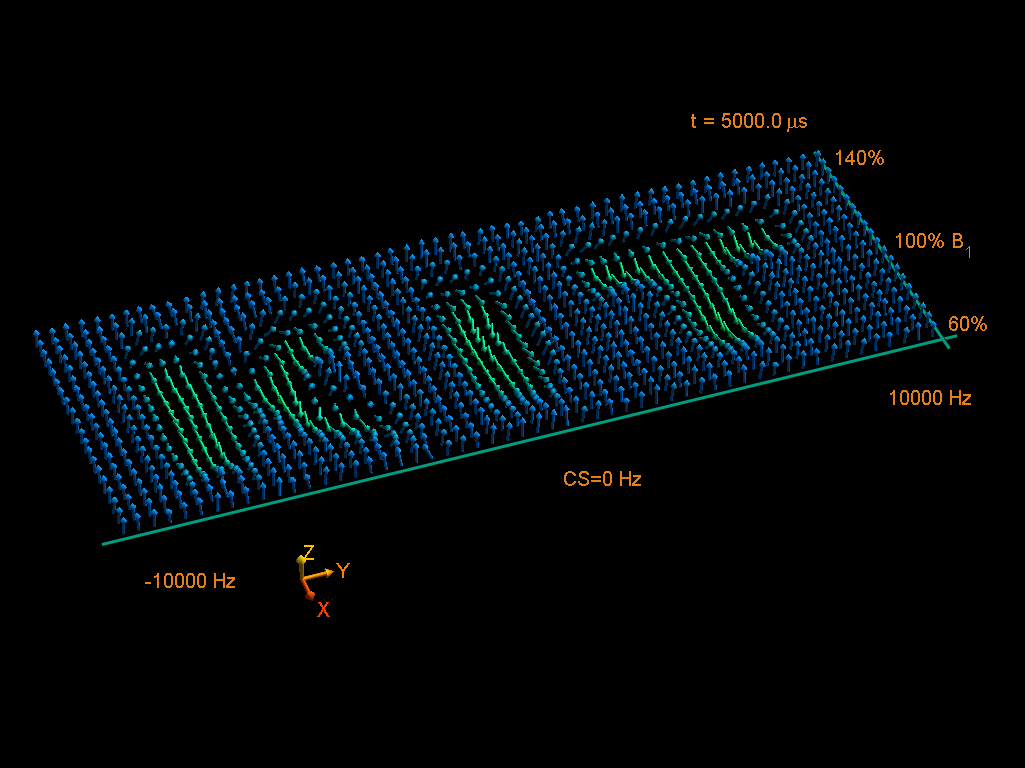
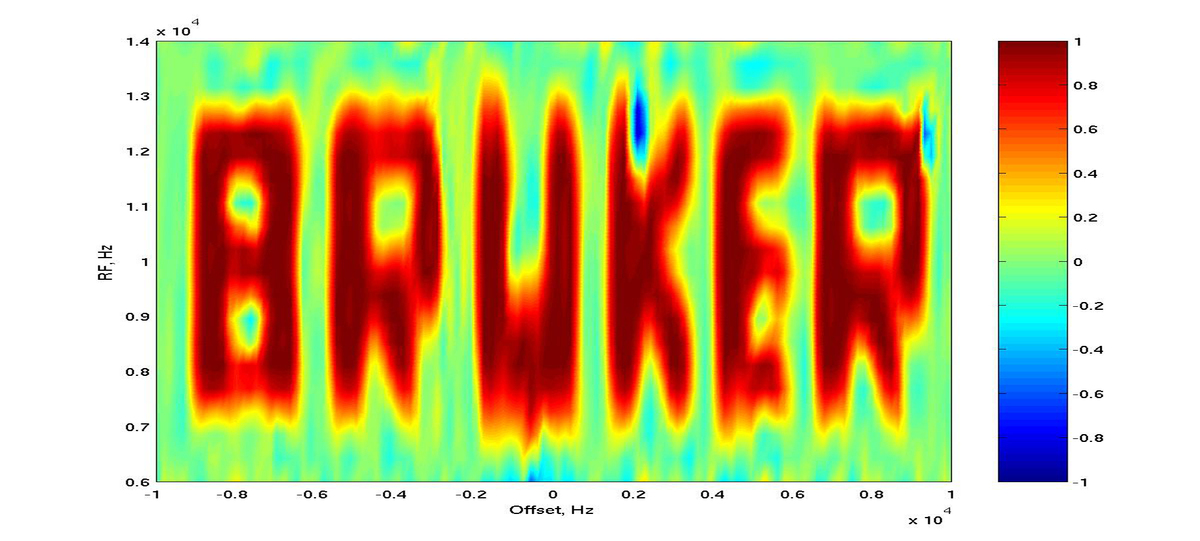
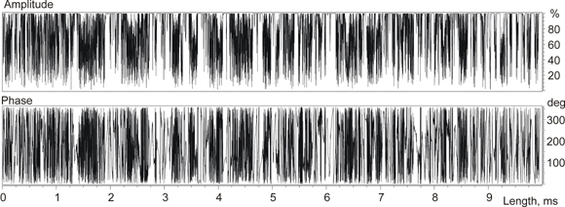
This way one can produce RF-pulses with stunning properties, like pulses with excitation profiles dependent in controllable predefined way on the RF amplitude the pulse is applied with. And though the pulse shape might look like a plain noise,
its excitation profile can be more than elaborate, as this simulation shows:
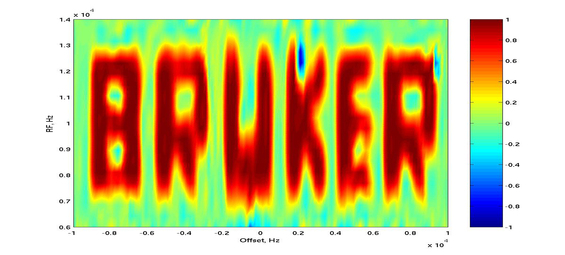
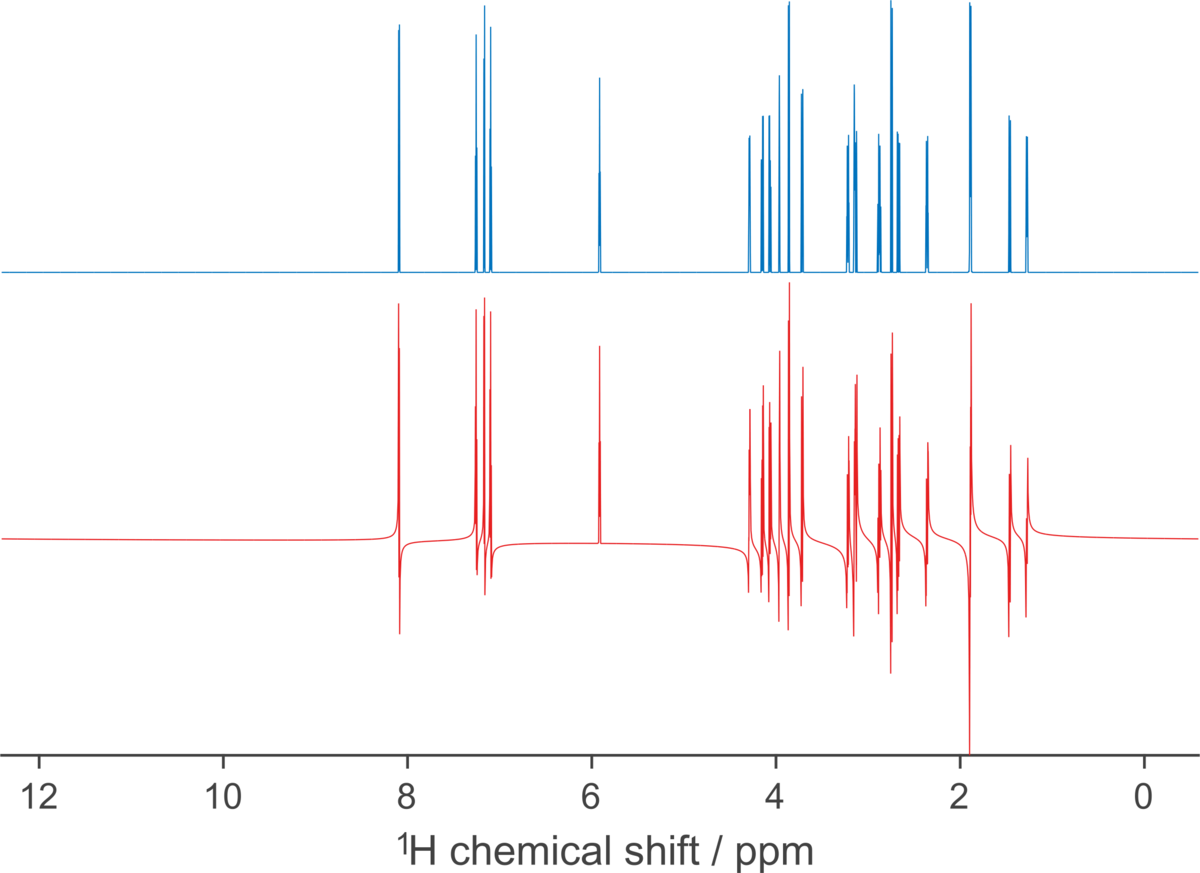
And this can be seen not only in simulations, but also can be implemented experimentally on spectrometer: